2022. 12. 10. 18:56ㆍ연구 동향
※ 요약하기 위해 포스팅을 했을 뿐,
개인적인 의견으로는 의미가 크지 않은 논문이므로 맨 마지막 한계 부분만 확인 바람
딥러닝을 이용한 주택 경매시장 예측에 관한 연구(2020, 김선아 및 전해정)
- 키워드: 주택, 경매, GARCH 모형, 딥러닝, 예측
- Keywords: Housing, Auction, Garch Model, Deep Learning, Prediction
개요
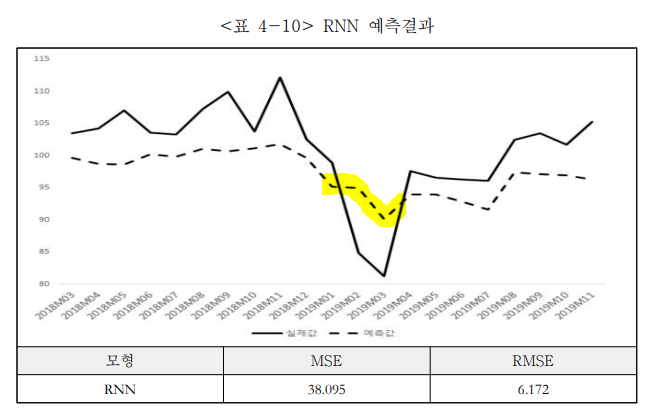
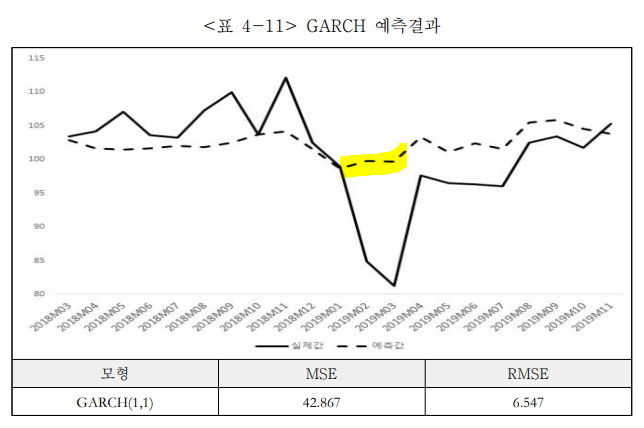
이 연구는 GARCH 모델과 딥러닝 RNN 모델로 주택 경매시장을 추정한 후 두 모델의 예측력을 비교하는 것을 목표로 한다. 사용된 변수는 아파트 경매 낙찰가율, 아파트 매매가격지수, 아파트 낙찰율, 회사채수익률, 소비자물가지수, 건축허가 여부 등이다. 결과적으로 딥러닝 RNN 모델(MSE: 38.095, RMSE: 6.172)이 GARCH 모델(MSE: 42.867, RMSE: 6.547) 보다 예측력이 우수하다는 것을 확인하였다.
목차
- 서론
- 선행연구
- 분석모형: 딥러닝, Basic RNN Cell, GARCH 모형
- 실증분석
- 결론
선행연구 고찰
주택시장 - 경매시장 간 상관관계에 대한 선행연구
- 장문덕, 박철형(2016): 시계열 분석 VAR 모형과 GARCH모형을 이용해 경매시장과 주택시장 간의 변동성 분석한 결과, 강남 지역의 경우 변동성에 의한 레버리지 효과가 있음을 확인함.
- 주택 매매시장과 경매시장 간의 상관관계에 관한 실증연구 - 글로벌 금융위기 전후를 중심으로(전해정, 2013): 글로벌 금융위기 전후의 주택 경매시장과 매매시장 간 상관관계를 VAR모형으로 분석한 결과, 금융위기 이전에는 음(-)의 관계, 이후에는 양(+)의 관계를 가지는 것을 확인함.
선행연구에서 제시한 경매 시장 영향 변수
- 서울시 주택 경매 낙찰 결정요인 로지스틱 회귀분석(김정선, 2015): 낙찰율을 높이는 요인으로 낙찰가비율, 개발여부, 유찰횟수, 낙찰율을 낮추는 요인은 임차인 유무, 건물이용, 경매범위, 감정가액, 인수권리유무
- 낙찰가 결정요인에 대한 가격결정모형(정가연, 2010): 대지지분, 평형, 유찰횟수, 응찰자수 등이 낙찰가격에 영향을 미침. 거시 경제 변수로 소비자 물가지수와 환율이 음의 상관관계, 총 통화량은 낙찰가격에 양의 상관관계를 줌.
- 부동산경매 위험요인의 낙찰가의 영향에 대한 확률계수모형(정성용, 2009): 영향의 크기는 건물상태, 유찰횟수(경매특성요인) >> 지역, 경과년수, 지수변동률(시장요인) 이었음.
선행연구에서는 선형 모형을 가정하므로 주택 시장의 비선형성을 반영하지 못한다는 한계가 있으므로, 비선형 추정 기법인 딥러닝 RNN 모형을 적용하여 기존 분석 방법인 GARCH와 예측력을 비교해보기로 함.
분석 모형
딥러닝 RNN 모델
- 입력 - 여러 개의 노드로 이루어진 Hidden Layer 1 - Hidden Layer 2 - Activation function(시그모이드, RLU 등) - 출력

- 순환신경망(RNN)은 순서가 있는 서열데이터를 처리하기 위한 모델로, 자료 순서에 따라 과거 정보를 학습하고 기억하여 현재 출력값을 예측함.
- x_t: t번째 입력 변수
- W: 가중치 행렬(weight matrix)로 학습을 통해 값이 정해짐.
- σ: 활성화 함수(Activation function)으로 이 논문에서는 시그모이드 함수를 사용함.
- h: 은닉 레이어의 출력

GARCH 모형
- 시계열 데이터에 있는 특정 기간에 변동이 매우 크게 나타나다가 어떤 기간에는 변동이 작게 나타나는 분산 군집현상이 나타나는데 이를 외부 충격으로 인한 영향이 발생하고 시간이 지나면서 소멸된다고 가정함.
- 이를 모형화한 것이 ARCH(오차항의 분산을 과거 시점 충격 함수로 설정)
- GARCH 모형은 분산을 과거 잔차항의 자승치와 조건부 분산의 일부를 시차의 선형으로 결함함. (차분을 이용)
- (σ_t)^2: 조건부 분산식
- (σ_t-1)^2: 이전 시차(t-1)의 조건부 분산
- (μ_t-1)^2: 이전 시차(t-1)의 오차 제곱

실증 분석
분석범위
- 아파트: 아파트 경매 낙찰가율 y(지지옥션), 아파트 매매가격지수 x1(국민은행), 아파트 낙찰율 x2(지지옥션)
- 금리 및 유동성: 회사채수익률 x3(한국은행)
- 경제성장: 소비자물가지수 x4(한국은행)
- 주택공급: 건축허가현황 주거용 x5(한국은행)
- 지역: 서울시
- 기간: 2002.01 ~ 2019.11

단위근 검정
거시경제변수에 대한 단위근 존재 여부 검정(ADF test, PP test): 차분 자료에서 모든 변수들의 단위근이 존재하지 않으므로 1차 차분 변수를 이용(비율 변수를 제외하고 로그차분 사용)
※ ADF test: 시계열 데이터의 안정성(Stationary)를 확인하기 위한 테스트, 안정성이 없으면 시간에 따라서 반복되는 패턴이 아니므로 패턴을 찾아내기 위한 딥러닝 모델은 의미가 없어짐.
※ PP test: 시계열 분석 에서 시계열이 차수 1로 적분 된다는 귀무가설을 검정하는 데 사용, 자기 상관 및 이분산성을 확인

분석 결과
RNN 모형
최적의 모수를 선택하기 위해 MSE, RMSE를 비교해가며 Dropout = 0.9, Epochs = 90, Neuron = [32,16,1]로 설정하였다.
※ 에폭(Epoch): 전체 단위가 학습되는 횟수로 에폭 값이 너무 크면 과적합, 작으면 과소적합(Underfitting) 문제 발생.
※ 드롭아웃(Dropout): 모델 성능을 향상 시키기 위해서 입력값 중 일부를 Drop-out(제외) 시킴. 과적합 방지가 목적.
실험 자료 중 학습용(training data set)과 검증용(test data set)의 비율은 9:1로 분할하였다.

GARCH 모형
GARCH(1,1) 모형을 통해 아파트경매낙찰가율은 전기의 아파트매매가격지수의 영향을 받은 것으로 알 수 있다.

※ AIC 검정: 여러 회귀 모형 중 가장 나은(과소적합, 과대적합 문제가 가장 적은) 모델을 찾아주는 성능 비교 방법
결론
시계열분석방법론인 GARCH모형 보다 딥러닝의 RNN모형의 예측력이 더 우수한 것을 실증적으로 알 수가 있었다.
한계
- 왜 활성화 함수가 Relu를 썼는지에 대한 설명이 없음. (그냥? 아니면 sigmoid 써 봤는데 성능이 안 나와서 뺀건지?)
- RNN 모형을 설정할 때 Layer 구조에 대해서 경험적으로 RMSE, MSE가 작은 숫자들을 갖다 썼을 뿐, 왜 이 모형이 되어야 하는지에 대한 설명과 근거가 부족함. (그저 모델을 노가다로 만든 것일 뿐)
- GARCH 모형과 비교해서 예측력(성능)이 좋다는 결론만 제시할 뿐, 왜 성능이 좋은지에 대해서는 설명할 수 없음. 따라서 시간이 지남에 따라 이 모델을 재사용이 가능할 지 불분명함. 즉, 예측력이 얼마나 지속될지 알 수 없음.
- 분산 분석이 제시되지 않기 때문에, 예측된 결과에 대해서 얼마나 신뢰할 수 있는지 알 수 없음.
- 데이터 중 학습용(Training set)과 검증용(Test set)의 비율이 9:1로, 2002년 ~ 2019년이라는 18년의 기간 중 예측 구간은 단 2년임. 학습데이터 수가 많으므로 Computational Cost 또한 많이 들었을 것으로 보임.
'연구 동향' 카테고리의 다른 글
| 부동산경매시장에서 매각가격은 할인되는가?(진남영 외 2인, 2010) (0) | 2022.12.21 |
|---|---|
| 물류센터 투자측면에서 입지선정 및 임대료 결정에 영향을 미치는 요인에 관한 연구(이남승, 2020) (1) | 2022.12.11 |
| 부동산 뉴스와 아파트 매매가격과 거래량 간의 관계에 대한 빅데이터 시계열 분석(2020, 전해정) (1) | 2022.12.07 |
| 경매특성 및 거시경제변수가 낙찰가율에 미치는 영향분석(2015, 이재욱 외 1인) (0) | 2022.12.06 |
| 경매시장의 진정한 낙찰가율 추정에 관한 연구(2009, 이해경 외 2인) (0) | 2022.11.30 |